This is a question that I’ve seen debated a few times, both in person and on the internet. It’s not quite in the same league as the immortal argument starter “airplane-on-a-treadmill”, but it has many of the same features.
To be clear about what I’m talking about, the question is whether having either flat or overinflated tyres would cause your car’s speedometer to display a significantly incorrect value (let’s say at least 5%). I’ve seen people advocating that people need to check their tyres, otherwise they could get false speeding tickets. For the sake of this discussion we’ll consider the simple case where the vehicle is traveling in a straight line, and the tyres operating with constant contact with the road, with no slip. Cornering and such will be left out.
At the heart is a couple of conflicting intuitions as to what happens.
The first intuition is that the height of the tyre, and hence the radius, will change as air pressure changes.
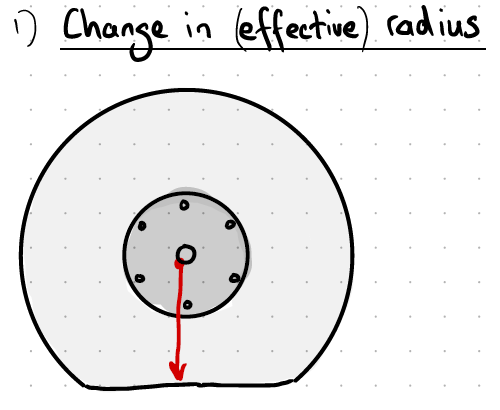
The second intuition is that regardless of the radius of the tyre, the circumference stays the same. And since each part of the tyre rolls against the ground, it doesn’t matter if it’s smushed down into a tank-track, the length covered by one rotation stays the same:
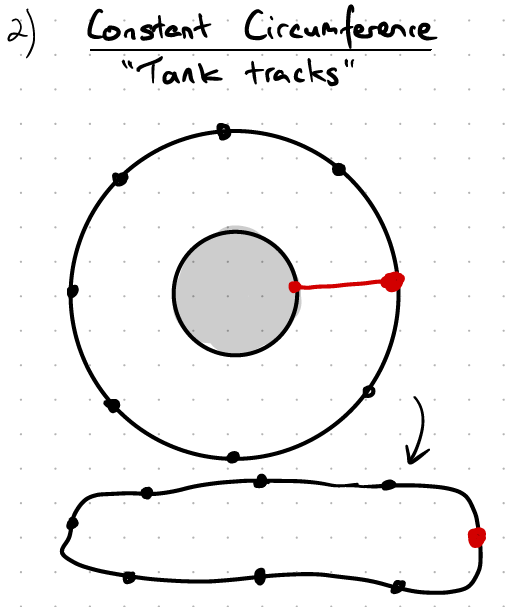
The third intuition of interest, is that the tyre will physically stretch as more air is inserted, thus changing both the radius and circumference:
These intutions pull in different ways, and focusing on only one can lead to the conclusion that the answer is easy and obvious. I was kinda fed up with seeing people on the internet arguing about it, and basically no-one doing the actual test. So I decided to do my own experiments and see what the results were.
I started by making a simple model to test the assumptions. I used a hot wire cutter to make two foam discs, and used a lasercut circle of wood in the middle as a hub. I then marked out a line on the edge, and measured how far it takes the tyre to roll one revolution along the table. As I thought, the results were significantly different if the wheel was “smushed” down by pressure, than if the wheel was rotating with no load:
But then I realised that modern tyres have steel bands “radials” in them, which act like the hoops on a barrel, and prevent expansion. So to replicate this, I wrapped one of my fake tyres in packing tape (which has amazing tensile strength):
When I did the tests again, I could clearly see that the difference between a loaded and unloaded tyre almost disappears:
So, does the real car behave in the same way as the fake tyres? In order to test this I needed to measure the car’s reported speed (from the speedometer), as well as a source of ground truth. I spent a while trying to get OBD-II data decoding on my car working well enough to log directly, but found it very frustrating dealing with the various devices.
I then realised that I was over-complicating this, and with a bit of searching I found an app for my phone that put a GPS overlay onto the camera feed. Then all I needed to do was tape my phone pointing at the speedo, and drive around. Then I could later look at any frame of the video and have a synchronized readout of both gauges.
(I’ve since figured out what I was doing wrong, and realised that rather than dealing with OBD protocols, I can sniff data directly from my car’s CANBUS at much higher rate. But the rest of this analysis is done with the video data).
I decided to try several “runs” in the car, with the tyres at various pressures far below and above normal ratings. My car is 230kPa, so I tried every pressure from 150-275kPa in 25kPa increments. This represents 65% to 120% of normal. (I didn’t really want to go much underneath 150kPa, as the tyres already looked fairly saggy to my eyes, and I didn’t want to risk damaging them and needing to buy a full replacement set).
I decided on a nice, fairly straight stretch of road with a high-ish speed limit ( 70km/h), with a service station at each end. That way if I had a problem with leaks or flats something I’d never t be far from help. Before each run I raised or lowered all four tyres to the same pressure, confirmed it with a handheld gauge, and drove, making sure to consistently record from the same starting point. Speed during the run will vary because there were a couple of traffic lights on the route, but I tried to stay just below the limit at a nice constant 60km/h to get as close as possible to measuring steady state.
After recording all the videos, I went back to the computer and started looking at the footage. Straight away I realised that it’s quite annoying to constantly pause and unpause video to make notes. Also it’s very difficult to pause at a regular gap (e.g. every 2 seconds), and by doing so I’d be introducing a lot of uncertainty into the measurement. This was a problem because there’s obviously a lag between the car’s speedo and the GPS, that I need to correct for.
To get good raw data out of the video, I used the free software “ffmpeg” in order to automatically “slice” the video at regular intervals into a folder full of still frames. According to my notes the magic incantation I used was:
“ffmpeg -i video_150kpa.MOV -filter:v fps=fps=1 ffmpeg%03d.png”
I then sat down in excel and transcribed the images to a spreadsheet. Once I had that I could analyze it in Jupyter notebooks with Numpy, Pandas, and Matplotlib.
The first problem was that there is clearly a scaling issue, as welll as a delay between the speedo velocity and the GPS. (Not unexpected, GPS tends to lag since it relies on calculation of recieved signals).
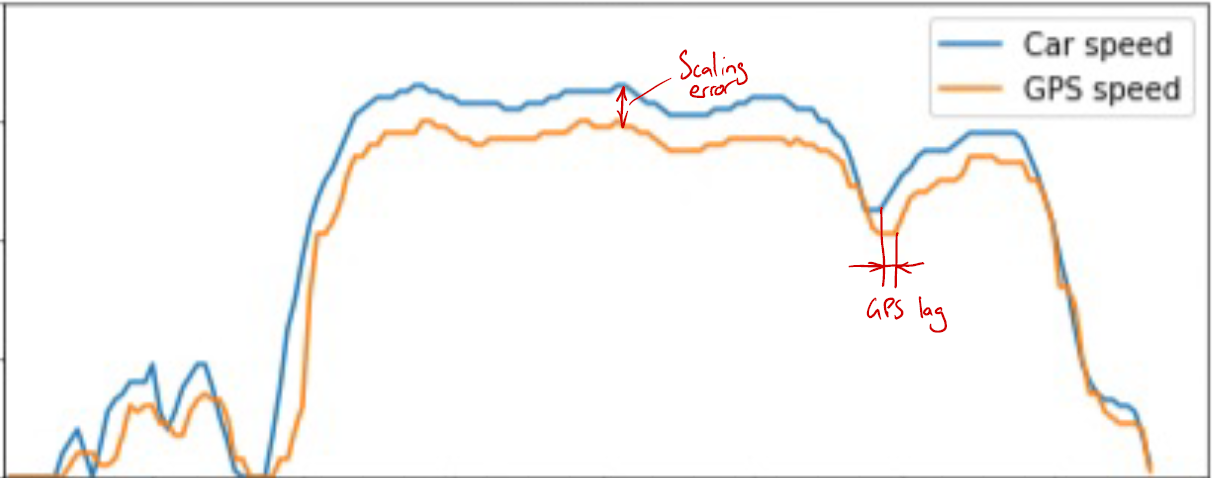
I calculated the mean squared error of the signal after applying various amounts of delay. You can see it’s quite consistent at 1sec for all the runs:
The second bit surprised me, the scaling always seems to be off by around 11%.
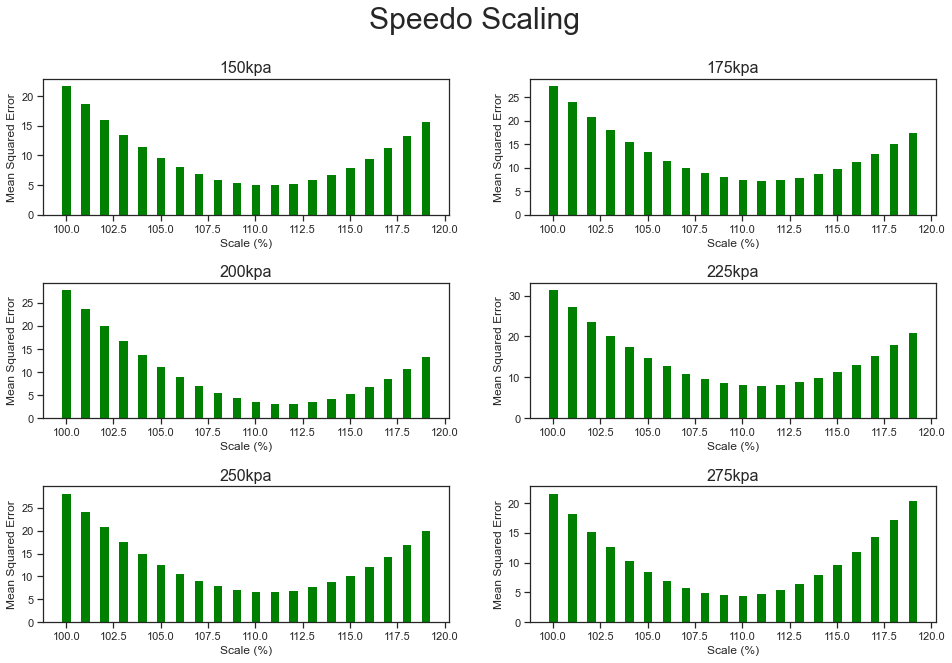(Later, when I analyzed raw CANBUS frames from the vehicle, I could see the speedo CANBUS values are actually different from the indiviudal tyre speed CANBUS values by a nice round 10%. I strongly suspect Toyota makes the speedo intentionally read exactly 10% fast to encourage more economical driving).
At any rate, if we now replot the data using the values of 1sec delay and 110% scaling, we can see the following:
I can’t see a difference in the above plot. But just to be sure, here’s a heatmap of all the data points, with GPS speed vs speedo speed. The diagonal line is the expected correlation, and the outer two lines are 2% higher and lower. You can see that vast majority of the data’s mass is within +-2% of the expected value.
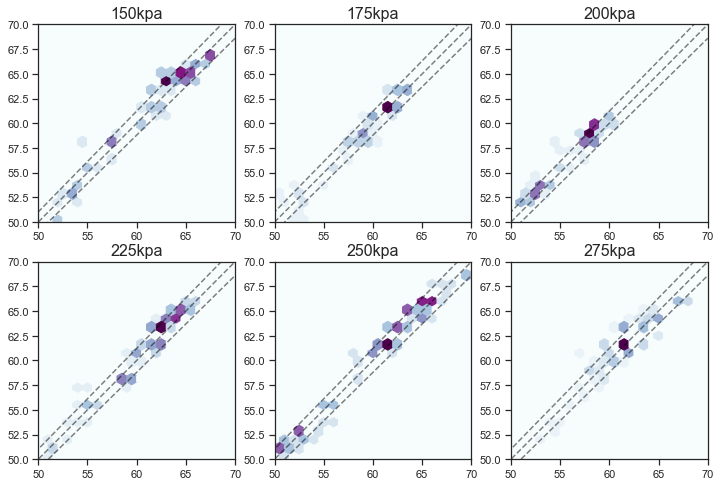
So it looks like there’s basically no difference between ridiculously flat and ridiculously inflated tyres as far as your speedo readout goes. Maybe other tyres would behave differently, but I doubt it.
This was a fun experiment to do, and it didn’t take more than a couple of evenings.
[Edit; I now have done more tests in Part 2!]
I polled my various DMs to get their opinions on which conditions which were most important, as well as required quantities of each ring. I did the design using Python and Jupyter notebooks. I wrote some code to make the shapes, write the text in a different colour, and put the variable diameter outline in place. To my mind that’s the killer feature, as the rings take up as little space as possible during both storage & play.
Tinkerings 